What Is The Largest Measurement

Unit of length used in astronomy

Parsec
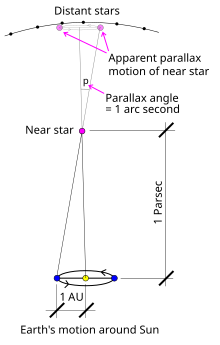A parsec is the distance from the Sun to an astronomical object that has a parallax angle of one arcsecond (not to scale)
General data
Unit system	astronomical units
Unit of measurement of	length/altitude
Symbol	pc
Conversions
1 pc in ...	... is equal to ...

metric (SI) units	3.0857×ten¹⁶ grand ~31 petametres
imperial & The states units	ane.9174×10^thirteen mi
astronomical units	two.06265 ×x⁵ au iii.26156 ly

The parsec (symbol: pc) is a unit of measurement of length used to measure the large distances to astronomical objects exterior the Solar Organisation, approximately equal to 3.26 light-years or 206,000 astronomical units (au), i.east. 30.nine trillion kilometres (19.ii trillion miles).^[a] The parsec unit is obtained by the use of parallax and trigonometry, and is defined every bit the altitude at which 1 au subtends an angle of one arcsecond^[ane] ( 1 / 3600 of a caste). This corresponds to 648000 / $π$ astronomical units, i.e. $one\,\mathrm {pc} =1/\tan \left({1}\ \mathrm {arcsec} \right)\,\mathrm {au}$ .^[2] The nearest star, Proxima Centauri, is almost 1.iii parsecs (four.2 lite-years) from the Lord's day.^[three] Most stars visible to the naked eye are within a few hundred parsecs of the Sunday, with the nigh distant at a few yard.^[4]

The give-and-take parsec is a portmanteau of "parallax of one 2d" and was coined by the British astronomer Herbert Hall Turner in 1913^[5] to brand calculations of astronomical distances from but raw observational data easy for astronomers. Partly for this reason, information technology is the unit of measurement preferred in astronomy and astrophysics, though the light-year remains prominent in popular science texts and common usage. Although parsecs are used for the shorter distances within the Milky Way, multiples of parsecs are required for the larger scales in the universe, including kiloparsecs (kpc) for the more than distant objects inside and around the Milky way, megaparsecs (Mpc) for mid-distance galaxies, and gigaparsecs (Gpc) for many quasars and the nearly distant galaxies.

In August 2015, the International Astronomical Spousal relationship (IAU) passed Resolution B2 which, as part of the definition of a standardized accented and apparent bolometric magnitude scale, mentioned an existing explicit definition of the parsec every bit exactly 648000 / $π$ au, or approximately 3.085677 581 491 3673 ×10¹⁶ metres (based on the IAU 2012 exact SI definition of the astronomical unit). This corresponds to the modest-angle definition of the parsec institute in many astronomical references.^[6] ^[seven]

History and derivation [edit]

The parsec is defined as being equal to the length of the adjacent leg (reverse leg being 1 AU) of an extremely elongated imaginary right triangle in space. The two dimensions on which this triangle is based are its shorter leg, of length i astronomical unit of measurement (the average Earth-Sun distance), and the subtended bending of the vertex opposite that leg, measuring one arcsecond. Applying the rules of trigonometry to these two values, the unit length of the other leg of the triangle (the parsec) can be derived.

I of the oldest methods used by astronomers to calculate the distance to a star is to record the difference in angle betwixt two measurements of the position of the star in the sky. The get-go measurement is taken from the World on one side of the Sunday, and the second is taken approximately half a year later, when the Earth is on the opposite side of the Sun. The distance between the 2 positions of the Earth when the 2 measurements were taken is twice the distance between the Earth and the Dominicus. The difference in bending between the two measurements is twice the parallax bending, which is formed by lines from the Sun and Earth to the star at the distant vertex. Then the distance to the star could exist calculated using trigonometry.^[8] The first successful published straight measurements of an object at interstellar distances were undertaken by High german astronomer Friedrich Wilhelm Bessel in 1838, who used this arroyo to summate the 3.5-parsec distance of 61 Cygni.^[ix]

Stellar parallax motion from annual parallax

The parallax of a star is divers every bit half of the angular distance that a star appears to motion relative to the celestial sphere as Globe orbits the Lord's day. Equivalently, it is the subtended angle, from that star's perspective, of the semimajor axis of the Earth'due south orbit. The star, the Sun and the Earth grade the corners of an imaginary correct triangle in space: the right angle is the corner at the Sun, and the corner at the star is the parallax angle. The length of the reverse side to the parallax angle is the distance from the Earth to the Sun (defined equally one astronomical unit, au), and the length of the adjacent side gives the distance from the sunday to the star. Therefore, given a measurement of the parallax bending, forth with the rules of trigonometry, the distance from the Sun to the star tin be found. A parsec is defined as the length of the side adjacent to the vertex occupied past a star whose parallax angle is one arcsecond.

The use of the parsec as a unit of altitude follows naturally from Bessel'due south method, because the altitude in parsecs can be computed but as the reciprocal of the parallax bending in arcseconds (i.east. if the parallax angle is ane arcsecond, the object is 1 pc from the Sun; if the parallax angle is 0.5 arcseconds, the object is 2 pc away; etc.). No trigonometric functions are required in this relationship because the very modest angles involved mean that the approximate solution of the skinny triangle tin exist applied.

Though information technology may have been used earlier, the term parsec was first mentioned in an astronomical publication in 1913. Astronomer Royal Frank Watson Dyson expressed his business organization for the demand of a proper noun for that unit of distance. He proposed the proper noun astron, simply mentioned that Carl Charlier had suggested siriometer and Herbert Hall Turner had proposed parsec.^[5] It was Turner's proposal that stuck.

Computing the value of a parsec [edit]

By the 2015 definition, 1 au of arc length subtends an angle of one″ at the centre of the circle of radius one pc. That is, 1 pc = 1 au/tan(ane") ≈ 206,264.8 au by definition.^[10] Converting from caste/minute/second units to radians,

{\frac {1{\text{ pc}}}{i{\text{ au}}}}={\frac {180\times lx\times lx}{\pi }}

, and

1{\text{ au}}=149\,597\,870\,700{\text{ m}}

(exact past the 2012 definition of the au)

Therefore,

\pi {\mbox{ pc}}=180\times 60\times threescore{\mbox{ au}}=180\times threescore\times threescore\times 149\,597\,870\,700=96\,939\,420\,213\,600\,000{\mbox{ m}}

(verbal by the 2015 definition)

Therefore,

one{\mbox{ pc}}={\frac {96\,939\,420\,213\,600\,000}{\pi }}=xxx\,856\,775\,814\,913\,673{\mbox{ m}}

(to the nearest metre)

Approximately,

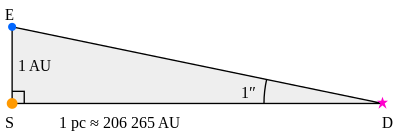
In the diagram in a higher place (non to scale), S represents the Sun, and Due east the Earth at one point in its orbit. Thus the distance ES is one astronomical unit (au). The bending SDE is one arcsecond ( 1 / 3600 of a degree) and so by definition D is a point in infinite at a altitude of ane parsec from the Sunday. Through trigonometry, the distance SD is calculated every bit follows:

{\begin{aligned}&\mathrm {SD} ={\frac {\mathrm {ES} }{\tan ane''}}\\[8pt]&\mathrm {SD} \approx {\frac {\mathrm {ES} }{1''}}={\frac {1\,{\mbox{au}}}{{\frac {1}{lx\times 60}}\times {\frac {\pi }{180}}}}={\frac {648\,000}{\pi }}\,{\mbox{au}}\approx 206\,264.81{\mbox{ au}}.\end{aligned}}

Considering the astronomical unit of measurement is defined to be 149597 870 700 grand,^[eleven] the following tin can exist calculated:

Therefore, 1 parsec	≈ 206264.806247 096 astronomical units
	≈ 3.085677 581 ×10¹⁶ metres
	≈ 30.856775 815 trillion kilometres
	≈ 19.173511 577 trillion miles

Therefore, if one ly ≈ ix.46×10^fifteen g,

Then 1 pc ≈ iii.261563 777 ly

A corollary states that a parsec is also the distance from which a disc ane astronomical unit in diameter must be viewed for information technology to have an angular diameter of one arcsecond (by placing the observer at D and a diameter of the disc on ES).

Mathematically, to calculate altitude, given obtained athwart measurements from instruments in arcseconds, the formula would be:

{\text{Distance}}_{\text{star}}={\frac {{\text{Distance}}_{\text{earth-sun}}}{\tan {\frac {\theta }{3600}}}}

where θ is the measured angle in arcseconds, Distance_earth-sun is a constant ( 1 au or 1.5813×x^−v ly). The calculated stellar altitude will be in the same measurement unit every bit used in Altitude_earth-sun (due east.g. if Distance_earth-sun = one au, unit for Altitude_star is in astronomical units; if Distance_world-sun = one.5813×10⁻⁵ ly, unit for Distance_star is in calorie-free-years).

The length of the parsec used in IAU 2015 Resolution B2^[12] (exactly 648000 / $π$ astronomical units) corresponds exactly to that derived using the pocket-size-angle adding. This differs from the classic inverse-tangent definition past nearly 200 km, i.due east. merely afterwards the 11th significant figure. As the astronomical unit was defined by the IAU (2012) as an exact SI length in metres, so now the parsec corresponds to an exact SI length in metres. To the nearest meter, the minor-bending parsec corresponds to 30856 775 814 913 673 g.

Usage and measurement [edit]

The parallax method is the key calibration step for distance determination in astrophysics; still, the accuracy of ground-based telescope measurements of parallax bending is limited to nearly 0.01″, and thus to stars no more than 100 pc distant.^[13] This is because the Globe's atmosphere limits the sharpness of a star'south image.^{[ citation needed ]} Space-based telescopes are not limited past this event and can accurately measure out distances to objects beyond the limit of ground-based observations. Between 1989 and 1993, the Hipparcos satellite, launched by the European Space Agency (ESA), measured parallaxes for nearly 100000 stars with an astrometric precision of about 0.97 mas, and obtained accurate measurements for stellar distances of stars up to chiliad pc away.^[xiv] ^[15]

ESA'southward Gaia satellite, which launched on 19 December 2013, is intended to measure ane billion stellar distances to within 20 microarcsecond, producing errors of 10% in measurements as far as the Galactic Center, nigh 8000 pc away in the constellation of Sagittarius.^[16]

Distances in parsecs [edit]

Distances less than a parsec [edit]

Distances expressed in fractions of a parsec usually involve objects within a single star organisation. So, for instance:

1 astronomical unit (au), the distance from the Lord's day to the Earth, is only under five×ten^{−half dozen} pc.
The most distant infinite probe, Voyager 1, was 0.000703 pc from Earth as of Jan 2019^[update]. Voyager one took 41 years to cover that distance.
The Oort cloud is estimated to be approximately 0.6 pc in diameter

Parsecs and kiloparsecs [edit]

Distances expressed in parsecs (pc) include distances between nearby stars, such equally those in the aforementioned spiral arm or globular cluster. A distance of 1,000 parsecs (3,262 ly) is denoted past the kiloparsec (kpc). Astronomers typically use kiloparsecs to express distances between parts of a galaxy, or within groups of galaxies. So, for example:

Ane parsec is approximately equal to 3.26 lite-years.
Proxima Centauri, the nearest known star to earth other than the sun, is about ane.three parsecs (iv.24 ly) abroad, by direct parallax measurement.
The distance to the open cluster Pleiades is 130±x pc ( 420±thirty ly) from us, per Hipparcos parallax measurement.
The middle of the Milky Way is more than than eight kiloparsecs (26,000 ly) from the World, and the Milky Way is roughly 34 kiloparsecs (110,000 ly) across.
The Andromeda Galaxy (M31) is about 780 kpc (two.5 million ly) away from the Earth.

Megaparsecs and gigaparsecs [edit]

Astronomers typically express the distances betwixt neighbouring galaxies and galaxy clusters in megaparsecs (Mpc). A megaparsec is i million parsecs, or near iii,260,000 light years.^[17] Sometimes, galactic distances are given in units of Mpc/h (as in "50/h Mpc", too written "50 Mpc h ⁻¹ "). h is a constant (the "dimensionless Hubble constant") in the range 0.5 < h < 0.75 reflecting the uncertainty in the value of the Hubble constant H for the rate of expansion of the universe: h = H / 100 km/s/Mpc . The Hubble constant becomes relevant when converting an observed redshift z into a altitude d using the formula d ≈ c / H × z .^[eighteen]

One gigaparsec (Gpc) is ane billion parsecs — 1 of the largest units of length ordinarily used. One gigaparsec is about three.26 billion ly, or roughly 1 / 14 of the distance to the horizon of the observable universe (dictated past the cosmic groundwork radiation). Astronomers typically use gigaparsecs to express the sizes of large-scale structures such as the size of, and distance to, the CfA2 Great Wall; the distances between milky way clusters; and the altitude to quasars.

For case:

The Andromeda Galaxy is almost 0.78 Mpc (2.5 million ly) from the Earth.
The nearest large galaxy cluster, the Virgo Cluster, is about sixteen.5 Mpc (54 million ly) from the Earth.^[nineteen]
The galaxy RXJ1242-xi, observed to have a supermassive black hole cadre like to the Galaxy's, is about 200 Mpc (650 meg ly) from the Earth.
The galaxy filament Hercules–Corona Borealis Smashing Wall, currently the largest known structure in the universe, is nigh three Gpc (ix.eight billion ly) beyond.
The particle horizon (the purlieus of the observable universe) has a radius of most 14 Gpc (46 billion ly).^[20]

Volume units [edit]

To make up one's mind the number of stars in the Milky Manner, volumes in cubic kiloparsecs^[b] (kpc³) are selected in various directions. All the stars in these volumes are counted and the total number of stars statistically determined. The number of globular clusters, grit clouds, and interstellar gas is determined in a like fashion. To determine the number of galaxies in superclusters, volumes in cubic megaparsecs^[b] (Mpc³) are selected. All the galaxies in these volumes are classified and tallied. The total number of galaxies can so be determined statistically. The huge Boötes void is measured in cubic megaparsecs.^[21]

In concrete cosmology, volumes of cubic gigaparsecs^[b] (Gpc³) are selected to determine the distribution of matter in the visible universe and to decide the number of galaxies and quasars. The Sun is currently the but star in its cubic parsec,^[b] (pc^three) simply in globular clusters the stellar density could be from 100–1000 pc⁻³ .

The observational volume of gravitational wave interferometers (e.g., LIGO, Virgo) is stated in terms of cubic megaparsecs^[b] (Mpc³) and is essentially the value of the constructive distance cubed.

In popular civilisation [edit]

The parsec was seemingly used incorrectly every bit a measurement of time past Han Solo in the beginning Star Wars film, when he claimed his ship, the Millennium Falcon "made the Kessel Run in less than 12 parsecs". The claim was repeated in The Force Awakens, but was clarified in Solo: A Star Wars Story, by stating the Millennium Falcon traveled a shorter distance (as opposed to a quicker fourth dimension) due to a more than unsafe route through hyperspace, enabled by its speed and maneuverability.^[22] It is too used ambiguously as a spatial unit in The Mandalorian.^[23]

In the book A Contraction in Time, "megaparsec" is Mr. Murry's nickname for his girl Meg.^[24]

In the 1955 science fiction brusk story by Isaac Asimov, 'Gamble', the outset hypersonic spaceship is named the "Parsec".

Run into as well [edit]

Attoparsec
Distance measures (cosmology)

Notes [edit]

^ 1 trillion here is short scale, ie. ten¹² (one million one thousand thousand, or billion in long scale).

^ ^a ^b ^c ^d ^east

1 pc^three	≈ 2.938×10⁴⁹ m³
1 kpc³	≈ ii.938×10⁵⁸ g³
i Mpc³	≈ ii.938×10⁶⁷ thousand³
1 Gpc³	≈ 2.938×ten⁷⁶ m³
1 Tpc³	≈ 2.938×ten⁸⁵ m³

References [edit]

^ "Cosmic Distance Scales – The Galaxy". Retrieved 24 September 2014.
^ B. Luque; F. J. Ballesteros (2019). "To the Dominicus and across". Nature Physics. 15 (12): 1302. Bibcode:2019NatPh..15.1302L. doi:ten.1038/s41567-019-0685-3.
^ Benedict, Thousand. F.; et al. "Astrometric Stability and Precision of Fine Guidance Sensor #3: The Parallax and Proper Motion of Proxima Centauri" (PDF). Proceedings of the HST Calibration Workshop. pp. 380–384. Retrieved 11 July 2007.
^ "Farthest Stars". StarDate. University of Texas at Austin. 15 May 2021. Retrieved 5 September 2021.
^ ^a ^b Dyson, F. Due west. (March 1913). "The distribution in space of the stars in Carrington'due south Circumpolar Catalogue". Monthly Notices of the Royal Astronomical Club. 73 (v): 342. Bibcode:1913MNRAS..73..334D. doi:10.1093/mnras/73.5.334. [paragraph xiv, page 342] Taking the unit of distance R* to be that respective to a parallax of 1″·0 [… Footnote:]
* There is need for a proper name for this unit of measurement of distance. Mr. Charlier has suggested Siriometer, but if the violence to the Greek linguistic communication can be overlooked, the discussion Astron might be adopted. Professor Turner suggests Parsec, which may exist taken as an abbreviated class of "a altitude corresponding to a parallax of one 2d".
^ Cox, Arthur Northward., ed. (2000). Allen'south Astrophysical Quantities (4th ed.). New York: AIP Press / Springer. Bibcode:2000asqu.book.....C. ISBN978-0387987460.
^ Binney, James; Tremaine, Scott (2008). Galactic Dynamics (2nd ed.). Princeton, NJ: Princeton Academy Press. Bibcode:2008gady.book.....B. ISBN978-0-691-13026-2.
^ Loftier Energy Astrophysics Science Archive Research Eye (HEASARC). "Deriving the Parallax Formula". NASA's Imagine the Universe!. Astrophysics Science Division (ASD) at NASA'due south Goddard Space Flying Heart. Retrieved 26 Nov 2011.
^ Bessel, F. W. (1838). "Bestimmung der Entfernung des 61sten Sterns des Schwans" [Determination of the altitude of the 61st star of Cygnus]. Astronomische Nachrichten. 16 (5): 65–96. Bibcode:1838AN.....sixteen...65B. doi:10.1002/asna.18390160502. Archived from the original on 24 June 2007.
^ B. Luque; F. J. Ballesteros (2019). "Title: To the Lord's day and beyond". Nature Physics. 15 (12): 1302. Bibcode:2019NatPh..15.1302L. doi:10.1038/s41567-019-0685-three.
^ International Astronomical Union, ed. (31 August 2012), "RESOLUTION B2 on the re-definition of the astronomical unit of measurement of length" (PDF), RESOLUTION B2, Beijing: International Astronomical Union, The XXVIII Full general Associates of the International Astronomical Wedlock recommends [adopted] that the astronomical unit of measurement be redefined to be a conventional unit of length equal to exactly 149597 870 700 m, in agreement with the value adopted in IAU 2009 Resolution B2
^ International Astronomical Union, ed. (xiii August 2015), "RESOLUTION B2 on recommended nothing points for the absolute and apparent bolometric magnitude scales" (PDF), RESOLUTION B2, Honolulu: International Astronomical Union, The XXIX General Assembly of the International Astronomical Union notes [4] that the parsec is defined every bit exactly (648 000/ $\pi$ ) au per the AU definition in IAU 2012 Resolution B2
^ Pogge, Richard. "Astronomy 162". Ohio State University.
^ "The Hipparcos Space Astrometry Mission". Retrieved 28 Baronial 2007.
^ Turon, Catherine. "From Hipparchus to Hipparcos".
^ "GAIA". European Space Agency.
^ "Why is a parsec 3.26 calorie-free-years?". Astronomy.com. 1 Feb 2020. Retrieved 20 July 2021. {{cite web}}: CS1 maint: url-condition (link)
^ "Milky way structures: the large scale construction of the nearby universe". Archived from the original on v March 2007. Retrieved 22 May 2007.
^ Mei, S.; Blakeslee, J. P.; Côté, P.; et al. (2007). "The ACS Virgo Cluster Survey. 13. SBF Distance Catalog and the Three-dimensional Construction of the Virgo Cluster". The Astrophysical Journal. 655 (1): 144–162. arXiv:astro-ph/0702510. Bibcode:2007ApJ...655..144M. doi:10.1086/509598. S2CID 16483538.
^ Lineweaver, Charles H.; Davis, Tamara G. (ane March 2005). "Misconceptions about the Large Bang". Scientific American. 292 (iii): 36–45. Bibcode:2005SciAm.292c..36L. doi:10.1038/scientificamerican0305-36. Archived from the original on 10 August 2011. Retrieved 4 February 2016.
^ Kirshner, R. P.; Oemler, A. Jr.; Schechter, P. L.; Shectman, South. A. (1981). "A million cubic megaparsec void in Bootes". The Astrophysical Periodical. 248: L57. Bibcode:1981ApJ...248L..57K. doi:10.1086/183623. ISSN 0004-637X.
^ "'Solo' Corrected One of the Nearly Infamous 'Star Wars' Plot Holes". Esquire. thirty May 2018.
^ Choi, Charlse (5 Nov 2019). "'Star Wars' Gets the Parsec Wrong Once more in 'The Mandalorian'". space.com . Retrieved half dozen May 2020.
^ "In "A Wrinkle in Fourth dimension," what is Mr. Murry'south nickname for Meg?". Retrieved 6 May 2020.

External links [edit]

Guidry, Michael. "Astronomical Distance Scales". Astronomy 162: Stars, Galaxies, and Cosmology. University of Tennessee, Knoxville. Archived from the original on 12 December 2012. Retrieved 26 March 2010.
Merrifield, Michael. "pc Parsec". Sixty Symbols. Brady Haran for the University of Nottingham.